Union-Find木(ユニオンファインド木)とはグループ分けを管理するデータ構造です。Union-Find木を用いることで、グループ同士の併合(Union)、ある要素がどのグループに属しているかを見つける操作(Find)を木構造を利用することで効率的にできるようになります。
Contents
Union-Find木の実装
Union-Find木におけるFind(ファインド)
以下のような配列が与えられたとします。
0 2 9 3 2 5 6 7 3 3
これは0番目(一番左を0番と数える)の要素の親は0(つまり自分自身が親)、1番目は2番目が親で2番目の親は9番目であることを示しています。続けると9番目の親は3番目で3番目の親は3番目です。つまり1番目の根(Root)は3番目の要素であることになります。Union-Find木において、ある要素の根を求めることを一般的にFind(ファインド)といいます。
Union-Find木にいける併合(Union)
Union-Find木では同じ根を持つ要素を同じグループとみなして管理します。
最初は配列の初期値では、すべての要素においてそれ自身が根となっています。つまり配列は以下のようになっています。
0 1 2 3 4 5 …
このなかからふたつの要素(aとb)を取り出し、aの根とbの根が同じでないなら、bの根の親をaの根とする操作をおこないます。両者の根が同じならば何もしません。
上の操作のように、別の根を持つ、別のグループの要素たちの根を同じにして同一グループとする操作を一般的にユニオンと言います。
C#で実装する
C#で実装してみることにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int[] arr = { 0, 1, 2, 3, 4 }; // 頂点は全部で5個。最初は自分自身が親なので arr[i] == i となる int[,] arr2 = { {3, 4}, // 3を4を併合(Union)する {2, 3}, {1, 2}, {0, 4}, }; for (int i = 0; i < arr2.GetLength(0); i++) { // rootA と rootB が同じでないなら、rootB の親を rootA とする int rootA = Find(arr2[i, 0], arr); int rootB = Find(arr2[i, 1], arr); if (rootB != rootA) arr[rootB] = rootA; } for (int i = 0; i < arr.Length; i++) Console.WriteLine($"{i}の親は{arr[i]}"); } static int Find(int i, int[] arr) { if (i == arr[i]) return i; else return Find(arr[i], arr); } } |
実行結果
|
1 2 3 4 5 |
0の親は0 1の親は0 2の親は1 3の親は2 4の親は3 |
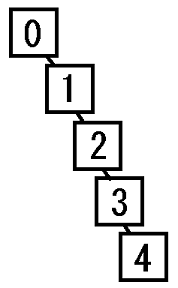
経路圧縮による動作改善
Findメソッドを少し改良して値を返すときに根を求める際にA[p]も更新しています。これによって次にpの根を求めるときに何回も再帰する必要がなくなり、処理速度を向上させることができます。これは経路圧縮と呼ばれています。
|
1 2 3 4 5 6 7 8 9 10 |
static int Find(int i, int[] arr) { if (i == arr[i]) return i; else { arr[i] = Find(arr[i], arr); return arr[i]; } } |
上記コードの実行結果は以下のようになります。
実行結果
|
1 2 3 4 5 |
0の親は0 1の親は0 2の親は1 3の親は1 4の親は1 |
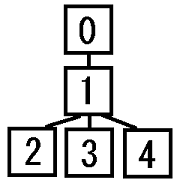
ランクによる動作改善
配列arrに加えて、もう一つ長さnの配列ranksを定義して、[1, …, 1]で初期化します。整数 i が属する木の、根から末端までの最大の長さをランクと定義してranksに格納します。
a の根と b の根を併合(Union)するとき、両者の根のランクに差があり、低いほうの根の親を高いほうの根とする場合は、高いほうのランクがさらに高くなることはないので、ランクは変わりません。逆に両者のランクが同じ場合はbの根の親をa の根とすることによって、aの根のランクが必ず1増えることになります。
Findメソッドは上と同じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
public class Program { static void Main() { int[] arr = { 0, 1, 2, 3, 4, 5 }; // 頂点は全部で6個。 int[] ranks = { 1, 1, 1, 1, 1, 1 }; int[,] arr2 = { {4, 5}, // 4を5を併合(Union)する {3, 4}, // 3を4を併合(Union)する {2, 3}, {1, 2}, {0, 5}, }; for (int i = 0; i < arr2.GetLength(0); i++) { // find(a) と find(b) が同じでないなら、ランクが低いほうの根の親をランクが高いほうの根とする。 // ランクが同じ場合、find(b) の親を find(a)の親とする。 int rootA = Find(arr2[i, 0], arr); int rootB = Find(arr2[i, 1], arr); if (rootB != rootA) { if (ranks[rootA] == ranks[rootB]) { arr[rootB] = rootA; ranks[rootA]++; // ランクが1増える } else if (ranks[rootA] > ranks[rootB]) // この場合はランクは変わらない arr[rootB] = rootA; else if (ranks[rootA] < ranks[rootB]) // この場合もランクは変わらない arr[rootA] = rootB; } } for (int i = 0; i < arr.Length; i++) Console.WriteLine($"{i}の親は{arr[i]}"); for (int i = 0; i < arr.Length; i++) arr[i] = find(i, arr); int[] roots = arr.Distinct().ToArray(); foreach (int i in roots) Console.WriteLine($"ルートは{i} ランクは{ranks[i]}"); } } |
実行結果
|
1 2 3 4 5 6 7 |
0の親は4 1の親は4 2の親は4 3の親は4 4の親は4 5の親は4 ルートは4 ランクは2 |
応用例
連結判定や閉路検出にも使えます。ルートがひとつしか存在しない場合はグラフは連結しているといえます。またグラフに辺を追加するときふたつの頂点のルートが同じであれば辺をつなぐことで閉路ができてしまうことに気づくことができます。
最小全域木
各辺に重み(コスト)がある場合、すべての頂点が辺によって連結していて、最小のコストで構成される全域木を最小全域木といいます。
クラスカル法とは最小全域木問題を解くアルゴリズムの一つです。辺の重みが小さい順にソートし、辺を追加したときに閉路ができないならば追加し、閉路ができる場合はとばして次の辺を考えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
using System; using System.Collections.Generic; using System.Linq; using static Program; public class Program { public class Edge { public Edge(int vertexNum1, int vertexNum2, int cost) { VertexNum1 = vertexNum1; VertexNum2 = vertexNum2; Cost = cost; } public int VertexNum1 = 0; public int VertexNum2 = 0; public int Cost = 0; } static void Main() { int[] arr = { 0, 1, 2, 3, 4, 5 }; // 頂点は6つ int[] ranks = { 1, 1, 1, 1, 1, 1 }; int[,] arr2 = { { 0, 1, 9 }, // 頂点0と頂点1を連結するときのコストは9 { 0, 5, 19 }, // 頂点0と頂点5を連結するときのコストは19 { 1, 5, 9 }, { 1, 4, 49 }, { 1, 3, 7 }, { 3, 5, 40 }, { 2, 5, 17 }, { 1, 2, 35 }, { 2, 3, 46 }, { 0, 2, 39 }, { 2, 4, 10 }, }; List<Edge> edges = new List<Edge>(); for (int i = 0; i < arr2.GetLength(0); i++) edges.Add(new Edge(arr2[i, 0], arr2[i, 1], arr2[i, 2])); // コストが小さい順にソート edges = edges.OrderBy(edge => edge.Cost).ToList(); List<Edge> useEdges = new List<Edge>(); foreach (Edge edge in edges) { int rootA = Find(edge.VertexNum1, arr); int rootB = Find(edge.VertexNum2, arr); // rootB != rootAなら閉路は形成されない if (rootB != rootA) { if (ranks[rootA] == ranks[rootB]) { arr[rootB] = rootA; ranks[rootA]++; } else if (ranks[rootA] > ranks[rootB]) arr[rootB] = rootA; else if (ranks[rootA] < ranks[rootB]) arr[rootA] = rootB; // グラフに追加した辺をリストに格納しておく useEdges.Add(edge); } } // 連結判定(ルートが1つだけか確認) for (int i = 0; i < arr.Length; i++) arr[i] = Find(i, arr); int[] roots = arr.Distinct().ToArray(); if (roots.Length == 1) { // コストと使用する辺を出力する Console.WriteLine($"最小全域木のコストは{useEdges.Sum(edge => edge.Cost)}"); Console.WriteLine($"使用する辺は"); foreach (Edge edge in useEdges) Console.WriteLine($"{edge.VertexNum1} - {edge.VertexNum2}"); } else Console.WriteLine("最小全域木は存在しない"); } } |
実行結果
|
1 2 3 4 5 6 7 |
最小全域木のコストは52 使用する辺は 1 - 3 0 - 1 1 - 5 2 - 4 2 - 5 |
