安定結婚問題と安定マッチング
安定結婚問題はデイヴィッド・ゲールと ロイド・シャプレイによって1962年に提示された問題です。同じ人数の男女がいて、各個人は各個人の好みに基づき異性全員のリストを持っています。
暫定的にペアを作った場合、互いに現在組んでいる相手よりも好きであるペアが存在する場合、これをブロッキングペアとか不安定対と呼びます。そしてブロッキングペアが存在せず、全員が個人合理性を満たすマッチングを安定マッチングといいます。
安定結婚問題の解は安定なマッチングです。そしてすべての場合において安定マッチングは必ず存在します。その安定マッチングを求める方法のひとつがゲールシャプレーアルゴリズムなのです。
以下のような問題が与えられたとします。
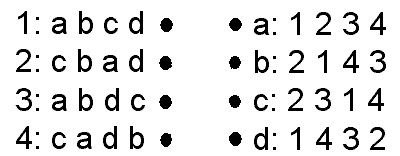
そして適当に結婚相手を選びます。
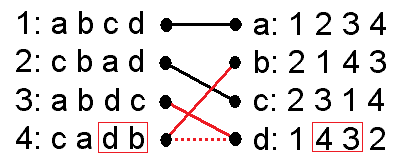
これをみると4は現在の婚約者であるbよりdとの結婚を望んでいます。dも現在の3より4との結婚を望んでいます。ハイ、駆け落ち成立です。
ではこのような駆け落ち(ブロッキングペア)が成立しないようにするにはどうすればよいのでしょうか?
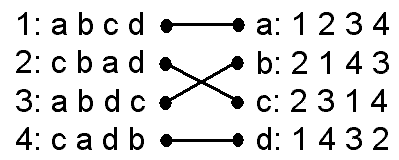
これなら駆け落ちされることはありません。全員がそれなりに幸せになれそうです。これが安定マッチングです。
ではどのようにすれば安定マッチングを実現することができるのでしょうか? その方法のひとつがゲールシャプレーアルゴリズムです。
ゲールシャプレーアルゴリズムとは?
ゲールシャプレーアルゴリズムは以下のような方法です。
婚約相手がいない男性1人が、これまでふられていない中から一番結婚したい女性に求婚する。
求婚された女性は相手がいない、または現在婚約関係にある男声よりもよい相手ならこれまでの相手とは婚約を破棄してその人と婚約する。そうでないなら求婚は拒否します。
これを何回も繰り返しすべての男性が誰かと婚約関係にあるなら処理は終了です。これで安定マッチングが得られます。
C#でコーディングする
C#でコーディングしてみることにします。
一番上に以下の3行が必要です。
|
1 2 3 |
using System; using System.Collections.Generic; using System.Linq; |
Parsonクラスの定義
0から始まる連番で男女にそれぞれ番号を与え、Queueの中に希望順に異性の番号を入れていきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
public class Parson { public Queue<int> Wants = new Queue<int>(); public int Number = 0; public int Keep = -1; public Parson(int number) { Number = number; } public void SetWants(int[] wants) { foreach (int i in wants) Wants.Enqueue(i); } } |
Mainメソッドの定義
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
public class Program { static void Main() { List<Parson> ms = new List<Parson>(); List<Parson> fs = new List<Parson>(); for (int i = 0; i < 4; i++) { ms.Add(new Parson(i)); fs.Add(new Parson(i)); } // 両者の希望順をセットする ms[0].SetWants(new int[] { 0, 1, 2, 3 }); ms[1].SetWants(new int[] { 2, 1, 0, 3 }); ms[2].SetWants(new int[] { 0, 1, 3, 2 }); ms[3].SetWants(new int[] { 2, 0, 3, 1 }); fs[0].SetWants(new int[] { 0, 1, 2, 3 }); fs[1].SetWants(new int[] { 1, 0, 3, 2 }); fs[2].SetWants(new int[] { 1, 2, 0, 3 }); fs[3].SetWants(new int[] { 0, 3, 2, 1 }); // 相手がいない男性が存在する限り処理を繰り返す while (ms.Count(_ => _.Keep == -1) > 0) { List<Parson> parsons = ms.Where(_ => _.Keep == -1).ToList(); foreach (Parson parson in parsons) { int fIndex = parson.Wants.Dequeue(); if (fs[fIndex].Keep == -1) { // 相手がいない parson.Keep = fIndex; fs[fIndex].Keep = parson.Number; Console.WriteLine($"成立:{parson.Number} - {fIndex}"); } else { // 相手がいる // 女性にとっての優先度を比較する int a = fs[fIndex].Wants.ToList().IndexOf(parson.Number); int b = fs[fIndex].Wants.ToList().IndexOf(fs[fIndex].Keep); // 略奪成功 if (a < b) { int old = fs[fIndex].Keep; parson.Keep = fIndex; fs[fIndex].Keep = parson.Number; ms[old].Keep = -1; Console.WriteLine($"破棄:{old} - {fIndex}"); Console.WriteLine($"略奪:{parson.Number} - {fIndex}"); } else { Console.WriteLine($"略奪失敗:{parson.Number} - {fIndex}"); } } } } Console.WriteLine("最終結果"); foreach (Parson male in ms) { Console.WriteLine($"{male.Number} - {male.Keep}"); } } } |
