巡回セールスマン問題とは、都市の集合と各都市間の距離が与えられ、全都市をちょうど1回ずつ訪れたのち出発した都市に戻ってくるような経路のうち最も短いものを求める問題です。
正確な値は取得できないのですが、最小全域木を使ってサラリーマン巡回問題の解の近似値を求めることができます。またこの方法は最悪でも最適値の2倍以下の値が得られます。
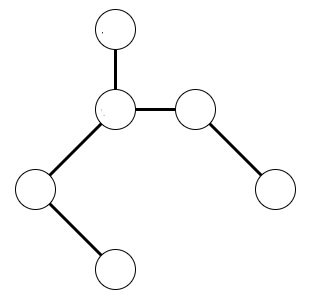
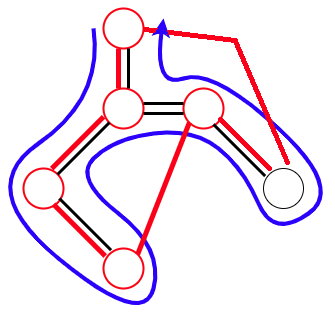
都市をグラフの頂点とみなし、最小全域木を求めます。そのあと最小全域木の辺を複製して二重にしたグラフを作り、都市を一筆書きで通過します。ただし既に訪れた都市には再度訪れないようにすることで巡回路を求めます。
Contents
最小全域木を求める
最初に最小全域木を求めるためのクラスを定義したいのですが、その前提になるNodeクラスとEdgeクラスを定義します。
NodeクラスとEdgeクラスの定義
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
using System; using System.Collections.Generic; using System.Linq; public class Node { public int NodeNumber = 0; public int Parent = -1; public Node(int num) { NodeNumber = num; } } public class Edge { public int NodeNumber1 = 0; public int NodeNumber2 = 0; public double Weight = 0; public bool Join = false; public Edge(int nodeNum1, int nodeNum2, double weight) { NodeNumber1 = nodeNum1; NodeNumber2 = nodeNum2; Weight = weight; } } |
MinimumSpanningTreeクラスの定義
最小全域木を求めるためのMinimumSpanningTreeクラスを定義します。
Node同士を連結させたときには親をつくります。GetParentメソッドは第一引数のノード番号(0から開始される)の一番上の親を求めます。親を上へ上へとたどっていき、その親が自分自身と同じ場合、それが一番上の親ということになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
public class MinimumSpanningTree { public int GetParent(int nodeNum, Node[] nodes) { int oldParent = nodeNum; int parent = nodes[nodeNum].Parent; while (true) { if (parent == -1) return -1; parent = nodes[oldParent].Parent; if (parent == oldParent) return parent; oldParent = parent; } } } |
GetSolutionメソッドの引数は都市のX座標とY座標のリストです。重みが小さいものから連結していきます。ただし双方に親がいる場合、その双方の一番上の親が同じ場合は連結すると閉路ができることを意味するので連結させません。グラフが連結であるためには閉路をつくる辺はあってもなくてもグラフが連結であることにかわりはないからです(つまり無くてよい)。
連結するときは親を決めます。双方はまだどことも連結していない場合はどちらかを適当に親にします。片方に親がいる場合はそれが親がいないものの親になります。双方に親がいて一番上の親が異なる場合は、一方の一番上の親が他方の一番上の親の親になります。
このメソッドは連結させるために必要な辺を返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
public class MinimumSpanningTree { public List<Edge> GetSolution(List<int> xs, List<int> ys) { int count = xs.Count; Node[] nodes = new Node[count]; for (int i = 0; i < count; i++) nodes[i] = new Node(i); List<Edge> edges = new List<Edge>(); for (int i = 0; i < count; i++) { for (int k = 0; k < count; k++) { if (i < k) { double d2 = Math.Pow(xs[i] - xs[k], 2) + Math.Pow(ys[i] - ys[k], 2); double d = Math.Sqrt(d2); edges.Add(new Edge(i, k, d)); } } } // 重みが小さい順にソート edges = edges.OrderBy(_ => _.Weight).ToList(); // 重みが小さい順に閉路ができないように連結していく foreach (Edge edge in edges) { int num1 = edge.NodeNumber1; int num2 = edge.NodeNumber2; if (nodes[num1].Parent == -1 || nodes[num2].Parent == -1) { int parentNum = Math.Max(nodes[num1].Parent, nodes[num2].Parent); if (parentNum != -1) // 大きいほうが-1でないならそれはどこかと連結している parentNum = GetParent(parentNum, nodes); // 後述 else // 両方がどことも連結していない parentNum = Math.Min(num1, num2); nodes[num1].Parent = parentNum; // 親を設定する nodes[num2].Parent = parentNum; edge.Join = true; } else // 両方に親がいる { int parentNum1 = GetParent(num1, nodes); int parentNum2 = GetParent(num2, nodes); if (parentNum1 != parentNum2) { edge.Join = true; int numTo = Math.Min(parentNum1, parentNum2); int numFrom = Math.Max(parentNum1, parentNum2); nodes[numFrom].Parent = numTo; } } } return edges.Where(_ => _.Join).ToList(); } } |
最小全域木を構成するために必要な辺のリストが返されたら、最小全域木の辺を複製して二重にしたグラフを作り、既に訪れた都市は飛ばして全都市を一筆書きで通過します。そのためには深さ優先探索すればいいですね。
最小全域木からサラリーマン巡回問題を解く
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
public class Program { // 都市は4つ。座標は (0, 0), (2, 2), (-1, 1), (0, - 2)とする static void Main() { int n = 4; List<int> xs = new List<int>() { 0, 2, -1, 0 }; List<int> ys = new List<int>() { 0, 2, 1, -2 }; MinimumSpanningTree tree = new MinimumSpanningTree(); var edges = tree.GetSolution(xs, ys); int count = xs.Count; bool[] isVisits = new bool[count]; int curNode = 0; Stack<int> stack = new Stack<int>(); List<int> path = new List<int>(); stack.Push(0); path.Add(0); while (true) { curNode = stack.Pop(); isVisits[curNode] = true; // 辺のうち curNode ではない側の頂点を求める。ただし一度訪問した場所は対象外とする List<Edge> edges1 = new List<Edge>(); edges1.AddRange(edges.Where(_ => _.NodeNumber1 == curNode)); List<Edge> edges2 = new List<Edge>(); edges2.AddRange(edges.Where(_ => _.NodeNumber2 == curNode)); foreach (Edge edge1 in edges1) { if (!isVisits[edge1.NodeNumber2]) { stack.Push(edge1.NodeNumber2); path.Add(edge1.NodeNumber2); } } foreach (Edge edge2 in edges2) { if (!isVisits[edge2.NodeNumber1]) { stack.Push(edge2.NodeNumber1); path.Add(edge2.NodeNumber1); } } if (stack.Count == 0) break; } // 巡回路を出力する Console.WriteLine(string.Join(" ", path.ToArray())); // 巡回路長を計算し出力する double ret = 0; int from = 0; int to = path[0]; for (int i = 1; i < n; i++) { from = to; to = path[i]; ret += Math.Sqrt(Math.Pow(xs[to] - xs[from], 2) + Math.Pow(ys[to] - ys[from], 2)); } ret += Math.Sqrt(Math.Pow(xs[to] - xs[path[0]], 2) + Math.Pow(ys[to] - ys[path[0]], 2)); Console.WriteLine(ret); } } |
出力結果
出力は以下のようになります。
|
1 2 |
0 2 3 1 11.8770543022872 |
本当の最適値は 11.048627177541 なのですが、出力された値はこの2倍以下になっているのがわかります。
