トーラス(ドーナツのような形)を描画します。
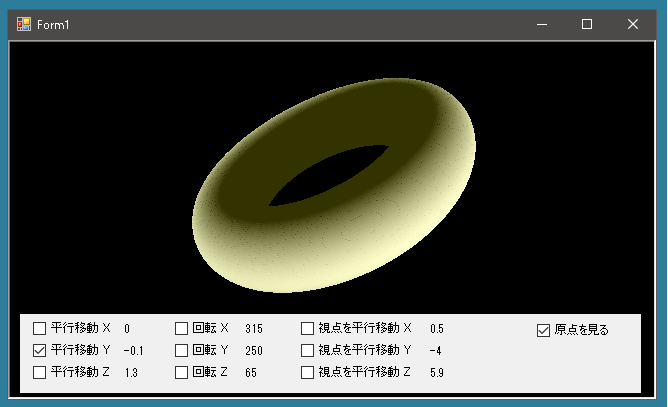
トーラスの表面は円周を回転して得られます。そこで円周を描画してこれを原点を中心に回転させます。自作メソッド DrawTaurus(double r1, double r2)の引数はr1が外側の大きな円の半径、r2が輪になっている部分の円周です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
public partial class Form1 : Form { private void glControlEx1_Paint(object sender, PaintEventArgs e) { GL.Clear(ClearBufferMask.ColorBufferBit | ClearBufferMask.DepthBufferBit); // 視点を変更する SetSight(EyeX, EyeY, EyeZ); GL.PushMatrix(); { GL.Translate(X, Y, Z); GL.Rotate(RotateX, 1, 0, 0); GL.Rotate(RotateY, 0, 1, 0); GL.Rotate(RotateZ, 0, 0, 1); DrawTaurus(2, 0.5); } GL.PopMatrix(); Lighting(); glControl.SwapBuffers(); } void DrawTaurus(double r1, double r2) { GL.Material(MaterialFace.Front, MaterialParameter.Ambient, Color.Yellow); int count = 128; double x = r1 * Math.Sqrt(2 * (1 - Cos(GetRad(360f / count)))); for(int k = 0; k < count; k++) { GL.PushMatrix(); GL.Rotate(360f / count * k, 0, 1, 0); GL.Translate(0, 0, r1 - r2); for(int i = 0; i <= count; i++) { GL.Rotate(360f / count, 1, 0, 0); GL.Begin(BeginMode.Quads); { GL.Normal3(Vector3.UnitZ); GL.Vertex3(-x / 2, r2, x / 2); GL.Vertex3(x / 2, r2, x / 2); GL.Vertex3(x / 2, r2, -x / 2); GL.Vertex3(-x / 2, r2, -x / 2); } GL.End(); } GL.PopMatrix(); } } } |
