問題です。
開始時点の x , y 座標と移動の歩数 N が与えられる。
以下の図のように時計回りに渦を巻くように移動を N 歩行った後の x , y 座標は?
マスの座標系は下方向が y 座標の正の向き、右方向が x 座標の正の向きとする。
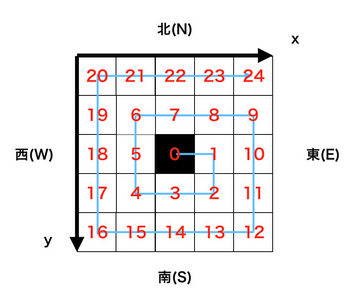
引用元:https://paiza.jp/works/mondai/a_rank_level_up_problems/a_rank_snake_move_step4
どうしょうか? どのようなコードを書けばいいのでしょうか?
Nを上、Sを下、Wを左、Eを右とすると移動はESWWNNEEESSSWWWWNNNNEEEEと続いていきます。連続する移動が繰り返すたびにだんだん増えていきます。
これはX方向とY方向をわけて考えればいいのでしょうか?
X方向だと
+1,(+1が1回)
0,(0が1回)
-1-1,(-1が2回)
0,0,(0が2回)
+1,+1,+1,(+1が3回)
0,0,0,(0が3回)
-1,-1,-1,-1,(-1が4回)
0,0,0,0,(0が4回)
+1,+1,+1,+1,+1(+1が5回)
0,0,0,0,0,(0が5回)
と続いていきます。これをXn = (nで表せる関数)で表わすことができればいいのですが、うまい方法が思いつきません。
結局、ああでもない、こうでもないと2時間くらい考えてもえがわからず回答を見ることにしました。
模範解答
模範解答をみると、移動の方向の規則性について以下のように解説しています。
移動の方向は、ESWN ESWN… と続いていく。
移動方向は全部で4種類だが、移動回数は同じではない。
ただ移動のマス数には規則性がある。それが11 22 33 44 … と続いていく。
そこで1回目の移動かどうかを管理するフラグを使えば実装可能とのことです。
n回移動した場合の座標を出力する関数は以下のようになります。引数はstartXが最初のX座標、startYが最初のY座標、nが移動回数です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
using System; class Program { static void func(int startX, int startY, int n) { int length = 1, now = 1, d = 1; bool first = true; int x = 0, y = 0; char[] direct = { 'N', 'E', 'S', 'W' }; for (int i = 0; i < n; i++) { int d0 = direct[d % 4]; if (d0 == 'N') y--; else if (d0 == 'S') y++; else if (d0 == 'E') x++; else if (d0 == 'W') x--; length--; if (!first && length == 0) { first = true; now++; length = now; d++; } else if (length == 0) { length = now; first = false; d++; } } Console.WriteLine("{0} {1}", startX + x, startY + y); } } |
うーん、これを思いつけというのは厳しいな。プログラマーであればすぐに気がつくのかもしれませんが、鳩レベルの脳みそしか持っていない管理人にとっては難しいです。
別解を考える
渦巻き状の処理であれば以前、このようなものを作ったことがあることを思い出しました。
ただ渦巻きの方向が違います。問題では中心から広がっていくように移動していくのですが、これは周囲から中心に向かって移動しています。どんなコードを書いていたのか見てみましたが、これは渦巻きの範囲が狭いから使える方法です。問題では移動の回数は100回を超えることはないということなので以下のようなコードで移動先の座標を求めることはできます。
及第点?それとも落第?
右に曲がることができる場合は右折する、できない場合は直進すればよいという規則性に気がつけば一応、これでよいはずです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
using System; using System.Linq; using System.Collections.Generic; using System.Drawing; class Program { static void func1(int startX, int startY, int n) { int x = startX, y = startY; List<Point> points = new List<Point>(); points.Add(new Point(x, y)); string direct = "N"; for (int i = 0; i <= n; i++) { if (i == 0) { continue; } if (direct == "N") { // 右へ曲がれるか? int newX = x + 1; if (!points.Any(point => point.X == newX && point.Y == y)) { direct = "E"; x = newX; } else { y--; } points.Add(new Point(x, y)); } else if (direct == "E") { // 右へ曲がれるか? int newY = y + 1; if (!points.Any(point => point.X == x && point.Y == newY)) { direct = "S"; y = newY; } else { x++; } points.Add(new Point(x, y)); } else if (direct == "S") { // 右へ曲がれるか? int newX = x - 1; if (!points.Any(point => point.X == newX && point.Y == y)) { direct = "W"; x = newX; } else { y++; } points.Add(new Point(x, y)); } else if (direct == "W") { // 右へ曲がれるか? int newY = y - 1; if (!points.Any(point => point.X == x && point.Y == newY)) { direct = "N"; y = newY; } else { x--; } points.Add(new Point(x, y)); } } Console.WriteLine("{0} {1}", x, y); } } |
n に100よりも少し大きな数をいれても結果はすぐに出力されます。しかしnがもっと大きな数だとどうでしょうか? 模範解答では1000万を超える数をいれても結果はすぐに出力されますが、このコードでは1万くらいまでならちょっと待たされるくらいで済みますが、2万だと相当待たされます。
points.Any()を繰り返しているわけですから時間がかかるのは当然といえば当然です。
速度を改善する
そこで二次元配列を使うのはどうでしょうか? 配列を使う以上、アクセス違反が起きないように気をつける必要がありますが、以下のコードであれば上記のコードよりは処理が速いです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 |
using System; class Program { static void func2(int startX, int startY, int n) { // 配列の外にアクセスしてしまわないように注意する int maxWidth = (int)Math.Ceiling(Math.Sqrt(n)) + 2; int sx = maxWidth / 2; int sy = maxWidth / 2; int x = sx; int y = sy; bool[,] map = new bool[maxWidth, maxWidth]; map[sx, sy] = true; string direct = "N"; for (int i = 0; i <= n; i++) { if (i == 0) { continue; } if (direct == "N") { // 右へ曲がれるか? int newX = x + 1; if (!map[newX, y]) { direct = "E"; x = newX; } else { y--; } map[x, y] = true; } else if (direct == "E") { // 右へ曲がれるか? int newY = y + 1; if (!map[x, newY]) { direct = "S"; y = newY; } else { x++; } map[x, y] = true; } else if (direct == "S") { // 右へ曲がれるか? int newX = x - 1; if (!map[newX, y]) { direct = "W"; x = newX; } else { y++; } map[x, y] = true; } else if (direct == "W") { // 右へ曲がれるか? int newY = y - 1; if (!map[x, newY]) { direct = "N"; y = newY; } else { x--; } map[x, y] = true; } } Console.WriteLine("{0} {1}", x - sx + startX, y - sy + startY); } } |
どっちが速い?
模範解答と2番目に自作したメソッドで実行時間を計測します(最初の自作メソッドは論外!)。
n は 4000 * 10000 です。結果は3倍強の差になりました。どちらも2秒以内なのでまあいいかなとも思いますが、模範解答には敵いませんでした。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
class Program { static void Main() { int x = 3; int y = 7; int n = 4000 * 10000; // いずれか片方を呼び出す // TestA(x, y, n); 400ms // TestB(x, y, n); 1300ms } static void TestA(int x, int y, int n) { System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch(); sw.Start(); func(x, y, n); sw.Stop(); Console.WriteLine(sw.ElapsedMilliseconds + " ms"); } static void TestB(int x, int y, int n) { System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch(); sw.Start(); func2(x, y, n); sw.Stop(); Console.WriteLine(sw.ElapsedMilliseconds + " ms"); } } |

お初です。
記事を拝見して興味が湧いたので私も書いてみました。
計算量はざっくりlog2 N回程度です。
上記の4000*10000歩の場合で26回の探索でした。
(問題の趣旨を勘違いして見当外れな結果なら申し訳ないです・・・)
C#は使ったことがないのでC++ですがソースコードはこちら
https://github.com/nboss476974/snake_move/blob/main/snake_move.cpp