累積和
累積和とは配列の任意の区間の総和を求めるためのアルゴリズムです。 繰り返し処理を使うと大きな計算量になってしまう区間の計算問題を、適切な前処理を行うことによって高速に行うことができます。
配列と累積和
int型の配列があり、そのなかから連続する K 個の整数の和の最大値を計算しなければならないときに重宝します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
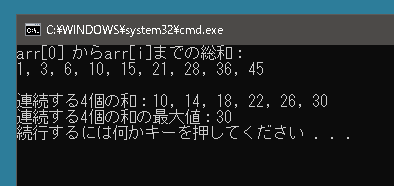
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int[] arr = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; int k = 4; int[] sums = new int[arr.Length]; int sum = 0; for (int i = 0; i < arr.Length; i++) { sum += arr[i]; sums[i] = sum; } Console.WriteLine($"arr[0] からarr[i]までの総和:"); Console.WriteLine(string.Join(", ", sums)); Console.WriteLine(); int[] results = new int[sums.Length - k + 1]; for (int i = 0; i + k - 1 < sums.Length; i++) { if (i == 0) results[0] = sums[i + k - 1]; else results[i] = sums[i + k - 1] - sums[i-1]; } Console.WriteLine($"連続する{k}個の和:{string.Join(", ", results)}"); Console.WriteLine($"連続する{k}個の和の最大値:{results.Max()}"); } } |
二次元累積和
二次元配列でも同じようなことをやってみることにします。
二次元配列の累積和は以下のように考えます。

これは以下の方法で計算できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
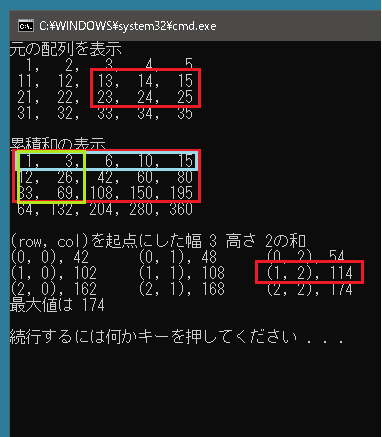
int[,] arr = { {1, 2, 3, 4, 5 }, {11, 12, 13, 14, 15 }, {21, 22, 23, 24, 25 }, {31, 32, 33, 34, 35 }, }; // この二次元配列に累積和が格納される int[,] sums = new int[arr.GetLength(0), arr.GetLength(1)]; for (int row = 0; row < arr.GetLength(0); row++) { int sum = 0; for (int col = 0; col < arr.GetLength(1); col++) { sum += arr[row, col]; sums[row, col] = sum; } } for (int col = 0; col < sums.GetLength(1); col++) { int sum = 0; for (int row = 0; row < sums.GetLength(0); row++) { sum += sums[row, col]; sums[row, col] = sum; } } |
一番上を0行目、一番左を0列目とすると、上から1行目、左から2列目を起点に幅3、高さ2であれば赤で囲われている部分から青と緑の部分を引きます。これだと二重に引いてしまった部分があるのでその部分を足します。計算式は 195-15-69+3 となり 114 が答えです。これは表示されている内容と一致しています。
二次元配列の連続する和の最大値
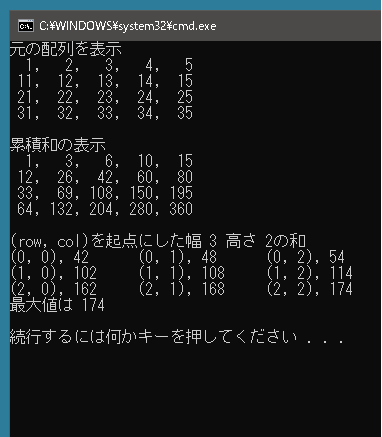
では二次元配列の累積和をつかって幅3、高さ2の連続する部分の和で最大のものを求めてみることにします。最大値は174になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 |
using System; using System.Collections.Generic; using System.Linq; public class Program { static void Main() { int[,] arr = { {1, 2, 3, 4, 5 }, {11, 12, 13, 14, 15 }, {21, 22, 23, 24, 25 }, {31, 32, 33, 34, 35 }, }; Console.WriteLine("元の配列を表示"); for (int row = 0; row < arr.GetLength(0); row++) { string[] temp = new string[arr.GetLength(1)]; for (int col = 0; col < arr.GetLength(1); col++) temp[col] = string.Format("{0,3}", arr[row, col]); Console.WriteLine(string.Join(", ", temp)); } Console.WriteLine(); int[,] sums = new int[arr.GetLength(0), arr.GetLength(1)]; for (int row = 0; row < arr.GetLength(0); row++) { int sum = 0; for (int col = 0; col < arr.GetLength(1); col++) { sum += arr[row, col]; sums[row, col] = sum; } } for (int col = 0; col < sums.GetLength(1); col++) { int sum = 0; for (int row = 0; row < sums.GetLength(0); row++) { sum += sums[row, col]; sums[row, col] = sum; } } Console.WriteLine("累積和の表示"); for (int row = 0; row < sums.GetLength(0); row++) { string[] temp = new string[sums.GetLength(1)]; for (int col = 0; col < sums.GetLength(1); col++) temp[col] = string.Format("{0,3}", sums[row, col]); Console.WriteLine(string.Join(", ", temp)); } Console.WriteLine(); int width = 3; int height = 2; Console.WriteLine($"(row, col)を起点にした幅 {width} 高さ {height}の和"); List<int> results = new List<int>(); for (int row = 0; row <= sums.GetLength(0)-height; row++) { for (int col = 0; col <= sums.GetLength(1)-width; col++) { results.Add(GetResults(sums, row, col, width, height)); Console.Write($"({row}, {col}),\t{GetResults(sums, row, col, width, height)}\t"); } Console.WriteLine(); } Console.WriteLine($"最大値は {results.Max()}"); Console.WriteLine(); } static int GetResults(int[,] sums, int row, int col, int width, int height) { // 起点がすでに配列の外 if (col >= sums.GetLength(1)) return 0; if (row >= sums.GetLength(0)) return 0; // どこを切り取るのか計算 int right; if (width - 1 + col < sums.GetLength(1)) right = width - 1 + col; else right = sums.GetLength(1) - 1; int bottom; if (height + row - 1 < sums.GetLength(0)) bottom = height + row - 1; else bottom = sums.GetLength(0) - 1; // 切り取った部分の和を取得 int ret = sums[bottom, right]; // 切り落とす部分の和を減算する if (row > 0) ret -= sums[row - 1, right]; if (col > 0) ret -= sums[bottom, col - 1]; // 2重に減算した部分を加算 if (col > 0 && row > 0) ret += sums[row - 1, col - 1]; return ret; } } |
実行結果
いもす法
いもす法は累積和を応用したアルゴリズムです。
配列といもす法
配列の連続する領域に同じ値を加算する処理ではいもす法で処理時間を短縮することができます。店内にどれだけお客さんがいるかを考えてみることにします。時間の経過とともにお客様は来たり帰ったりを繰り返します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
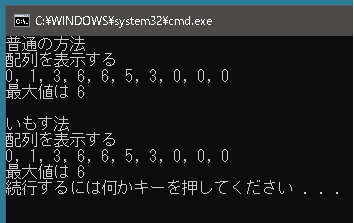
public class Program { static void Main() { List<StayOfGuests> stayOfGuests = new List<StayOfGuests>(); stayOfGuests.Add(new StayOfGuests(1, 5, 1)); // 引数 1_入店時間 2_退店時間 3_人数 stayOfGuests.Add(new StayOfGuests(2, 6, 2)); stayOfGuests.Add(new StayOfGuests(3, 7, 3)); Console.WriteLine("普通の方法"); int[] ints1 = new int[10]; foreach (StayOfGuests guest in stayOfGuests) { // guest.ExitTimeには退店しているので加算してはならない for (int i = guest.EnteringTime; i < guest.ExitTime; i++) ints1[i] += guest.CountGuests; } Console.WriteLine("配列を表示する"); Console.WriteLine(string.Join(", ", ints1)); Console.WriteLine("最大値は " + ints1.Max()); } } |
上の例では時間を表わす配列のサイズは10と小さく、店に出入りする時間の幅も小さいので、処理に時間がかかりすぎることはありません。しかし、実際には時間を表わす配列のサイズはもっと大きく、店に出入りする時間の幅も大きい場合はどうなるでしょうか?
いもす法とは、区間の入口と出口で要素分の加算・減算を行ない累積和を求める方法です。この方法だと配列のある区間内の値を何度も書き換える必要がなくなるので、処理の高速化が期待できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
public class Program { static void Main() { List<StayOfGuests> stayOfGuests = new List<StayOfGuests>(); stayOfGuests.Add(new StayOfGuests(1, 5, 1)); stayOfGuests.Add(new StayOfGuests(2, 6, 2)); stayOfGuests.Add(new StayOfGuests(3, 7, 3)); Console.WriteLine("いもす法"); int[] ints2 = new int[10]; foreach (StayOfGuests guest in stayOfGuests) { // 区間の入口(出店時間)と出口(退店時間)で要素分の加算・減算を行なう ints2[guest.EnteringTime] += guest.CountGuests; ints2[guest.ExitTime] -= guest.CountGuests; } // ここで累積和を計算すると上記と同じ結果が得られる int[] sum = new int[10]; for (int i = 0; i < ints2.Length; i++) { int prev = 0; if (i != 0) prev = sum[i - 1]; sum[i] = prev + ints2[i]; } Console.WriteLine("配列を表示する"); Console.WriteLine(string.Join(", ", sum)); Console.WriteLine("最大値は " + sum.Max()); } } |
当然のことながら実行結果は同じになります。
二次元上のいもす法
二次元上のいもす法は、区間の入口と出口を以下のように設定します。ここでは [2, 2]から[4, 5] まで 2を加算し、[4, 4]から[6, 7] まで 3を加算する処理をおこなっています。
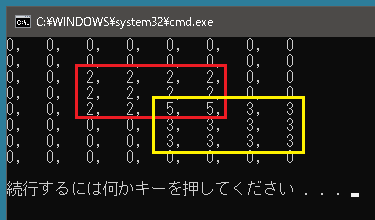
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
public class Program { static void Main() { int rowMax = 8; int colMax = 8; int[,] arr = new int[rowMax, colMax]; // [2, 2] [4, 5] まで 2を加算する arr[2, 2] += 2; arr[2, 5 + 1] -= 2; arr[4 + 1, 2] -= 2; arr[4 + 1, 5 + 1] += 2; // [4, 4] [6, 7] まで 3を加算する arr[4 , 4] += 3; arr[6+1, 4] -= 3; //arr[4, 7+1] -= 3; // 配列の範囲外はなにもしない //arr[6 + 1, 7 + 1] += 3; // 配列の範囲外はなにもしない // 累積和を計算する for (int row = 0; row < rowMax; row++) { for (int col = 0; col < colMax; col++) { if (col > 0) arr[row, col] += arr[row, col - 1]; } } for (int col = 0; col < colMax; col++) { for (int row = 0; row < rowMax; row++) { if (row > 0) arr[row, col] += arr[row - 1, col]; } } // 結果を出力する for (int row = 0; row < rowMax; row++) { int[] temp = new int[arr.GetLength(1)]; for (int col = 0; col < colMax; col++) temp[col] = arr[row, col]; Console.WriteLine(string.Join(", ", temp)); } Console.WriteLine(); } } |
