今回も巡回セールスマン問題を解きます。
Contents
巡回セールスマン問題を2-opt法で解く
2-opt法とは以下のような方法です。
初期解を適当に作る。
一定の回数か、解があまり改善されなくなるまで以下を繰り返す
巡回路を成す辺を 2 本選び、その辺をつなぎ変えることを考える。
つなぎ変えることによって巡回路長が短くなるならつなぎ変える。
短くならないなら何もしない。
都市の座標を管理するためのNodeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
using System; using System.Collections.Generic; using System.IO; using System.Linq; public class Node { static int _no = 0; public int X = 0; public int Y = 0; public int ConnectCount = 0; public int NodeNumber = 0; public Node(int x, int y) { X = x; Y = y; NodeNumber = _no; // 生成した順に通し番号をつける _no++; } } |
TwoOptクラスの定義
2-opt法で巡回セールスマン問題を解くクラスを定義します。
以下は2つの辺を選ぶための乱数を生成するメソッドです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
public class TwoOpt { uint _state = 813; uint XorShift32() { uint x = _state; x ^= x << 13; x ^= x >> 17; x ^= x << 5; _state = x; return _state; } } |
以下は生成された2つの辺を選ぶメソッドです。常に a より b のほうが大きくなるようにします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
public class TwoOpt { void PickTwo(int n, ref int a, ref int b) { while (true) { a = (int)(XorShift32() % n); b = (int)(XorShift32() % n); if (a > b) { int c = a; a = b; b = c; } if (!(a + 1 < b) || (a == 0 && b == n - 1)) continue; return; } } } |
一定の回数だけ乱数で2つの辺を選んで、辺を入れ替えたとき短くなるのであれば辺を入れ替える処理を示します。配列の外にアクセスしてしまう場合はスタート地点に戻ってくるように剰余を利用しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
public class TwoOpt { public List<Node> GetSolution(List<Node> tour, int q, ref double pathLength) { int n = tour.Count; for (int i = 0; i < q; i++) { // 適当に2つの辺を選ぶ int a = 0; int b = 0; PickTwo(n, ref a, ref b); int nextA = (a + 1) % n; int nextB = (b + 1) % n; // 2つの辺を入れ替えることで短くなるか? double before = 0; before += Math.Sqrt(Math.Pow(tour[a].X - tour[nextA].X, 2) + Math.Pow(tour[a].Y - tour[nextA].Y, 2)); before += Math.Sqrt(Math.Pow(tour[b].X - tour[nextB].X, 2) + Math.Pow(tour[b].Y - tour[nextB].Y, 2)); double after = 0; after += Math.Sqrt(Math.Pow(tour[a].X - tour[b].X, 2) + Math.Pow(tour[a].Y - tour[b].Y, 2)); after += Math.Sqrt(Math.Pow(tour[nextA].X - tour[nextB].X, 2) + Math.Pow(tour[nextA].Y - tour[nextB].Y, 2)); // 短くなる場合は実際に2つの辺を入れ替える if (after < before) { tour.Reverse(a + 1, b - a); // 暫定的に得られた解を表示させてみる string tourText = string.Join(" ", tour.Select(_ => _.NodeNumber).ToArray()); double length = GetPathLength(tour); Console.WriteLine($"{i}:\t{length}"); Console.WriteLine(tourText); } } pathLength = GetPathLength(tour); return tour; } } |
得られた経路の長さを取得する処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public class TwoOpt { double GetPathLength(List<Node> tour) { int n = tour.Count; double pathLength = 0; for (int m = 0; m < n; m++) { Node from = tour[m]; Node to = tour[(m + 1) % n]; double d2 = Math.Pow(to.X - from.X, 2) + Math.Pow(to.Y - from.Y, 2); pathLength += Math.Sqrt(d2); } return pathLength; } } |
解を求める
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
public class Program { static void Main() { List<Node> nodes = new List<Node>() { new Node(2, 0), new Node(1, 1), new Node(2, 1), new Node(1, 2), new Node(0, 0), new Node(-1, 0), new Node(-2, 0), new Node(-1, 1), new Node(-1, 2), new Node(1, -2), new Node(2, -2), new Node(-1, -2), new Node(0, -2), new Node(-1, -1), new Node(2, 2), new Node(1, -1), }; int q = 1000; System.Diagnostics.Stopwatch stopwatch = new Stopwatch(); stopwatch.Start(); TwoOpt twoOpt = new TwoOpt(); double pathLength = 0; List<Node> newTour = twoOpt.GetSolution(nodes, q, ref pathLength); stopwatch.Stop(); Console.WriteLine($"時間(ms): {stopwatch.ElapsedMilliseconds}"); Console.WriteLine(pathLength); Console.WriteLine(string.Join(" ", newTour.Select(_ => _.NodeNumber).ToArray())); } } |
都市の数 16 で1000回ループさせてみると以下のようになりました。1000回ループでも11回しか更新されていません。
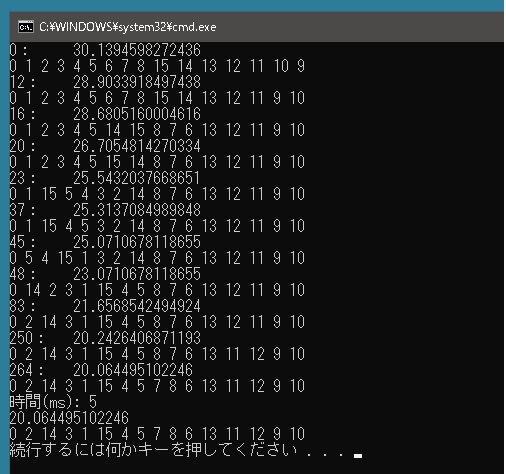
実行にはそんなに時間はかかりませんでした。2500都市 1000回ループでも 0.1 秒かかりません。
巡回セールスマン問題を禁断探索法で解く
禁断探索法は以下のような方法です。
解を適当に作り、暫定解 X とする。
最良解 B を X で初期化する。禁断リストを空で初期化するとともに、禁断リストのサイズの上限 TL を決める
一定の回数、以下を繰り返す
暫定解 X を少し変更したもの (X の近傍) であり、禁断リストに含まれていない解のうち最も良い解を求め、これを暫定解とする。
暫定解 X を禁断リストの先頭に加える。禁断リストのサイズが上限を超えた場合は禁断リストに含まれている最も古い解を削除する。
最良解 B を解として出力する
禁断リストを用いることによって、同じようなところを何度も探索するのを少なくなることが期待できます。
ここでは「X の近傍」を巡回路 X に含まれる2本の辺を繋ぎ変えたものと定義します。そして「禁断リスト」には繋ぎ変えた辺の端点のうち巡回路Xの先頭に最も近い都市 t を入れます。これは、t を端点として持つ辺を繋ぎ変えて解を更新するとしばらくのあいだ、t を端点として持つ辺は繋ぎ変えないことを意味しています。
都市の座標を管理するためのNodeクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
using System; using System.Collections.Generic; using System.Linq; public class Node { public int X = 0; public int Y = 0; public int NodeNumber = 0; static int _number = 0; public Node(int x, int y) { X = x; Y = y; NodeNumber = _number; // 生成した順に通し番号をつける _number++; } } |
TabuSearchクラスの定義
巡回セールスマン問題を禁断探索法で解くためのTabuSearchクラスを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
public class TabuSearch { // 都市と都市のあいだの距離を求める double GetDistance(Node a, Node b) { return Math.Sqrt(Math.Pow(a.X - b.X, 2) + Math.Pow(a.Y - b.Y, 2)); } // 巡回経路長を求める public double GetPathLength(List<Node> tour) { int n = tour.Count; double pathLength = 0; for (int i = 0; i < n; i++) pathLength += GetDistance(tour[i], tour[(i + 1) % n]); return pathLength; } } |
禁断探索法で解を求める処理を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
public class TabuSearch { public List<Node> GetSolution(List<Node> tourNode, int q, int tl) { int n = tourNode.Count; double length = GetPathLength(tourNode); // 暫定解の巡回経路長を記憶する Queue<int> tabuList = new Queue<int>(); // 禁断リスト // 暫定解 tourNode の近傍を全探索する for (int i = 0; i < q; i++) { int aBest = 0, bBest = 0; double diff = double.MaxValue; for (int a = 0; a < n; a++) { // 禁断リストにあるものは対象外 if (tabuList.Any(_ => _ == tourNode[a].NodeNumber)) continue; for (int b = a + 2; b < n; b++) { // 繋ぎ変える 2 辺の端点が重複してしまう場合を除外する if (a == 0 && b == n - 1) continue; double d_before = GetDistance(tourNode[a], tourNode[(a + 1) % n]) + GetDistance(tourNode[b], tourNode[(b + 1) % n]); double d_after = GetDistance(tourNode[a], tourNode[b]) + GetDistance(tourNode[(a + 1) % n], tourNode[(b + 1) % n]); double tmp_diff = d_after - d_before; // 短くできる場合は解の候補 if (tmp_diff < diff) { diff = tmp_diff; aBest = a; bBest = b; } } } // 先に解の候補をタブーリストに追加する tabuList.Enqueue(tourNode[aBest].NodeNumber); if (tabuList.Count > tl) tabuList.Dequeue(); // これを暫定解とする tourNode.Reverse(aBest + 1, bBest - aBest); double tmp_length = GetPathLength(tourNode); // 現在よりも短くできる場合は巡回経路長を更新する if (tmp_length <= length) length = tmp_length; } return tourNode; } } |
解を求める
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
public class Program { static void Main() { int q = 100; int tl = 5; List<Node> tourNode = new List<Node>() { new Node(2, 0), new Node(1, 1), new Node(2, 1), new Node(1, 2), new Node(0, 0), new Node(-1, 0), new Node(-2, 0), new Node(-1, 1), new Node(-1, 2), new Node(1, -2), new Node(2, -2), new Node(-1, -2), new Node(0, -2), new Node(-1, -1), new Node(2, 2), new Node(1, -1), }; System.Diagnostics.Stopwatch stopwatch = new System.Diagnostics.Stopwatch(); stopwatch.Start(); TabuSearch tabuSearch = new TabuSearch(); List<Node> newTour = tabuSearch.GetSolution(tourNode, q, tl); double pathLength = tabuSearch.GetPathLength(newTour); stopwatch.Stop(); Console.WriteLine($"時間(ms): {stopwatch.ElapsedMilliseconds}"); Console.WriteLine(pathLength); Console.WriteLine(string.Join(" ", newTour.Select(_ => _.NodeNumber).ToArray())); } } |
都市の数 16、禁断リストのサイズの上限 5 で1000回ループさせてみると以下のようになりました。
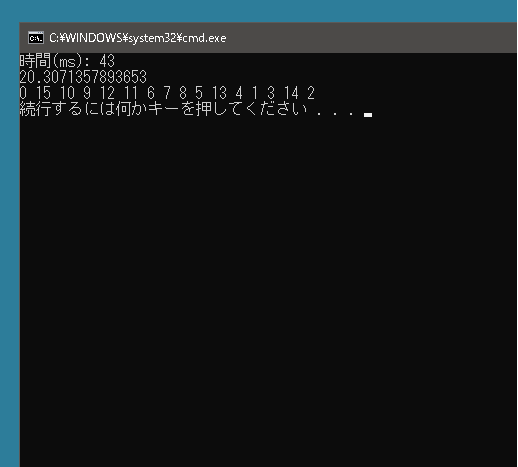
実行にはそんなに時間はかかりませんが、2-opt法と比べると時間がかかります。200都市 150回ループだと約 1 秒かかります。
